Análisis factorial (AF)

Conceptualización

El análisis factorial (AF) es un conjunto de técnicas estadísticas usadas, entre otras áreas, en psicometría, para identificar las dimensiones subyacentes en un conjunto de variables observadas. Busca descubrir patrones de relaciones entre múltiples variables, agrupando aquellas que comparten varianza común. Esta varianza compartida sugiere que las variables podrían estar midiendo un mismo constructo psicológico (factor latente).

En psicometría, el AF tiene varios propósitos:

• Validar un test: comprobar si un test refleja uno o varios constructos.
• Encontrar relaciones entre factores de pruebas distintas: validez convergente y discriminante.
• Desarrollar teorías sobre posibles constructos latentes a partir de datos (por ejemplo, teorías sobre inteligencia o personalidad).
• Reducir la complejidad de los datos concentrando la información en menos dimensiones.

El análisis factorial fue propuesto por Spearman en 1904 para validar su Teoría bifactorial de la inteligencia, si bien el precedente teórico lo sentó Galton en 1883. En 1931, Thurstone amplió esta técnica para su teoría de las Aptitudes Mentales Primarias.

Glosario de conceptos

Antes de explicar en qué consiste, voy a listar algunos conceptos fundamentales en el análisis factorial, así como sinónimos que se utilicen de forma habitual.

• Factores latentes ($F_k$): son variables hipotéticas o constructos no directamente observables que se infieren a partir de varias variables observadas. El objetivo de un análisis factorial es identificar y estimar estos factores que explican la correlación entre las variables medidas en un estudio.

  • Sinónimos: variables latentes, dimensiones latentes, constructos.

• Pesos factoriales ($a_{pi}$): coeficientes que indican la influencia de cada factor latente sobre una variable observable. Se aplican en la fórmula que expresa una variable $X_p$ como combinación de factores más un error.

  • Sinónimos: cargas factoriales, pesos, factor loadings, $a_{pi}$.

• Matriz de correlaciones ($R$): tabla que representa las correlaciones entre todas las variables observables. Por ejemplo, una matriz de dimensión $p \times p$ si hay $p$ variables. Constituye el insumo base para el análisis factorial, que busca reproducir esta matriz mediante un número reducido de factores.

  • Sinónimos: Correlation matrix, $R$.

• Correlación ($r$ o $\rho$): grado de asociación lineal entre dos variables, normalmente medida por el coeficiente de Pearson que va de $-1$ a $+1$. El análisis factorial asume que la correlación entre las variables se explica por factores comunes.

  • Sinónimos: coeficiente de correlación, r.

• Unicidad ($u_p^2$ o $(1 - h_p^2$)): parte de la varianza de cada variable observable que no se explica por los factores comunes, sino por factores específicos y/o error. Se representa con $u_p^2$ o $(1 - h_p^2)$. Indica cuánta varianza de una variable queda fuera de la explicación por los factores comunes.

  • Sinónimos: uniqueness, varianza específica, residual variance.

  La unicidad se compone de dos conceptos:

  • Error: componente de la variable que no se atribuye a los factores comunes, abarcando error de medición o características específicas de la variable. Explica que los factores no suelan predecir perfectamente la variable. Aparece como $u_p E_p$ en la ecuación factorial.
    • Sinónimos: término de error, error term, residuo, variable aleatoria.
  • Parte específica (factor específico): es la porción de la varianza de la variable que no se comparte con otras (tampoco con los factores comunes), pero que no se considera estrictamente “error aleatorio”. Puede ser un rasgo muy particular que sólo esa variable mide.
    • Sinónimos: factor único, componente específico.

• Varianza ($\sigma^2$): medida de dispersión de una variable respecto a su media. En el análisis factorial, a menudo se estandarizan las variables ($\sigma^2 = 1$) para repartir esa varianza en comunalidad y unicidad.

  • Sinónimos: variance, $\sigma^2$.

Tipos

Dependiendo de la finalidad, el análisis factorial se divide en:

1. Análisis Factorial Exploratorio (AFE): si parto de los datos para inducir o explorar una teoría.
2. Análisis Factorial Confirmatorio (AFC): si parto de una teoría previa para comprobar si se ajusta a los datos.

El AFE permite explorar la estructura latente sin hipótesis fuertes, mientras que el AFC verifica hipótesis teóricas específicas sobre cómo se relacionan variables y factores.

Cada uno utiliza métodos de estimación y procedimientos específicos, pero ambos comparten la idea de relacionar variables observadas con factores latentes.

Variables, factores y unicidad

En análisis factorial clásico, las variables observables como los ítems de un test pueden explicarse por una serie de factores latentes (constructos) y un término de error (o unicidad).

• Factores latentes: constructos como la inteligencia espacial, verbal, numérica, rasgos de personalidad, etc.
• Unicidad: la parte exclusiva de cada variable, que no se comparte con las demás y que, por tanto, no es explicada por los factores comunes. También incluye error de medida.
• Variable observable: la puntuación empírica que obtenemos (por ejemplo, la puntuación de un ítem).

Así, cada variable observable se compone de una parte debida a uno o varios factores comunes y de su unicidad, que engloba su parte específica y el error de medida.

A modo ilustrativo, imagina un conjunto de 9 ítems en un test que varían de manera que se pueden agrupar en tres grupos. Esto significa que tres factores latentes explican las varianzas de los 9 ítems:

Dicho de otra manera, cada medida observable se explica por una unicidad, pero también un factor latente que explica la correlación entres variables medidas observables:

Correlación entre variables observadas

La correlación entre dos variables cualesquiera, $X_p$ y $X_q$, en el modelo factorial, proviene de los factores latentes que ambas comparten. Se obtiene como la suma de los productos de sus cargas factoriales:

$$\rho(X_p, X_q) = \sum_{i=1}^k a_{p i} \times a_{q i},$$

donde:

• $a_{p i}$ es la carga de la variable $p$ en el factor $i$
• $a_{q i}$ es la de la variable $q$.

En otras palabras, las variables se correlacionan en la medida en que coinciden en sus factores comunes. Si dos variables no comparten factores, sus cargas factoriales en esos factores no coinciden y la correlación tenderá a ser cero.

Análisis factorial exploratorio (AFE)

El AFE, de forma general, intenta descubrir la estructura latente sin imponer una teoría inicial muy rígida sobre qué ítems deben agruparse. El procedimiento de un análisis factorial exploratorio sigue los siguientes pasos:

1. Crear una matriz de correlaciones inicial
2. Extraer factores
3. Rotar factores
4. Interpretar los factores
5. Obtener las cargas factoriales y puntuaciones factoriales

A continuación explico cada paso en detalle.

1. Crear una matriz de correlaciones inicial

Este paso consiste en entender, de forma aproximada, si hay correlación entre las variables. En caso de que no haya correlaciones, si los datos parecen un caos, no merece la pena continuar con el proceso.

	E1	E2	E3	V1	V2	V3	N1	N2	N3
E1	1.00
E2	0.73	1.00
E3	0.72	0.94	1.00
V1	0.04	0.15	0.10	1.00
V2	0.05	0.06	0.08	0.83	1.00
V3	0.10	0.16	0.09	0.82	0.87	1.00
N1	0.04	0.14	0.12	0.04	0.05	0.10	1.00
N2	0.15	0.16	0.08	0.15	0.16	0.18	0.79	1.00
N3	0.12	0.06	0.09	0.10	0.06	0.07	0.96	0.78	1.00

En caso de que los datos parezcan mostrar algún patrón, se procede a utilizar técnicas que permiten a encontrar los factores latentes.

2. Extraer factores

Este paso consiste en utilizar técnicas estadísticas para determinar la cantidad de factores que pueden explicar las correlaciones entre las variables observadas. Es decir, a partir de la matriz de correlaciones inicial, encontrar una Matriz de cargas factoriales que muestra los pesos factoriales ($a_{ik}$).

Matriz de correlaciones ($R$)

	E1	E2	E3	V1	V2	V3	N1	N2	N3
E1	1.00	0.73	0.72	0.04	0.05	0.10	0.04	0.15	0.12
E2	0.73	1.00	0.94	0.15	0.06	0.16	0.14	0.16	0.06
E3	0.72	0.94	1.00	0.10	0.08	0.09	0.12	0.08	0.09
V1	0.04	0.15	0.10	1.00	0.83	0.82	0.05	0.10	0.06
V2	0.05	0.06	0.08	0.83	1.00	0.87	0.10	0.16	0.07
V3	0.10	0.16	0.09	0.82	0.87	1.00	0.05	0.18	0.07
N1	0.04	0.14	0.12	0.05	0.10	0.05	1.00	0.79	0.96
N2	0.15	0.16	0.08	0.10	0.16	0.18	0.79	1.00	0.78
N3	0.12	0.06	0.09	0.06	0.07	0.07	0.96	0.78	1.00

👉

Factores

	F-E	F-V	F-N
E1	0.71	0.05	0.03
E2	0.83	0.04	0.14
E3	0.79	0.12	0.09
V1	0.04	0.75	0.14
V2	0.09	0.76	0.21
V3	0.07	0.81	0.11
N1	0.11	0.12	0.89
N2	0.17	0.14	0.90
N3	0.09	0.19	0.76

Sin embargo, primero hay que realizar pruebas previas que arrojen luz sobre la distribución de los datos.

Autovalor (λ)

Antes de proceder a explicar el proceso de extracción de factores, tengo que explicar qué es un autovalor. El cálculo y uso de los autovalores es un paso clave en la extracción de factores.

Un autovalor ($\lambda$) refleja la cantidad de variación que un factor explica de cada variable observadas. Es decir, cada factor latente tiene un autovalor. Dicho de otra manera: un autovalor es un escalar que se utiliza para representar la magnitud de la transformación que se aplica a los autovectores.

La fórmula para calcular el autovalor es:

$$\lambda_K = \sum^p_{i=1} \cdot \; a^2_{iK}$$

Donde:

• $\lambda_K$ es el autovalor para la variable $k$
• $a_{iK}$ es la carga factorial de la variable $i$ en el factor $K$.
  • El subíndice $i$ (que va de 1 a $p$) representa las variables.
  • El subíndice $K$ (entre 1 y $k$) representa al factor específico (el factor número $K$).

Relación entre carga ($a$) y autovalor ($\lambda$)

Cada factor tiene muchas cargas factoriales (una por variable). Sin embargo, cada factor tiene sólo un autovalor. De hecho, el autovalor de un factor es la suma de los cuadrados de todas esas cargas factoriales.

Los conceptos de carga ($a$) y autovalor ($\lambda$) responden a distintas preguntas:

• Cargas factoriales: ¿cómo se relaciona cada variable concreta con el factor?
• Autovalor: ¿Cuánta varianza total explican todas esas relaciones sumadas?

Por ello, cuando el análisis factorial muestra un factor con cargas relativamente altas en varias variables, el autovalor de ese factor sube, indicando que explica más varianza global en la matriz de correlaciones.

Una vez calculado el autovalor, se puede calcular qué proporción de la varianza es explicada por cada factor. Para ello, se utiliza la siguiente fórmula:

$$\% \sigma^2(F_k) = \frac{\lambda_k}{p} \times 100$$

donde:

• $\% \sigma^2(F_k)$ se refiere a la proporción de la varianza de un factor $k$.
• $p$ es la cantidad de variables, y también la varianza total del sistema. Si hay $p$ variables estandarizadas, la varianza total del sistema de variables es $p$. Puesto que son variables estandarizadas ($\sigma = 1$), cada variable tiene varianza $1$, y hay $p$ variables. Por eso la varianza total es igual a la cantidad de variables ($p$).
• $\lambda_k$ es el autovalor del factor $k$.

Cada autovalor refleja la varianza explicada por su factor correspondiente. Si el autovalor es grande, significa que ese factor explica más varianza de las variables.

Por ejemplo, mira la siguiente tabla:

Factor	Autovalor ($\lambda$)	% varianza autovalor ($\% \sigma^2(F_k)$)	% acumulado
A	1.938	32.307	32.307
B	1.235	20.585	52.892
C	0.906	15.100	67.992
D	0.760	12.667	80.659
E	0.642	10.604	91.363
F	0.518	8.637	100.000

Como se puede ver, cada factor tiene un autovalor que refleja cuánta varianza conjunta de las variables explica ese factor. El Factor A tiene un autovalor de 1.938. Esto significa que exlica el 1.938 de la varianza en las variables. Esto supone el 32,307% de varianza, ya que $\frac{1.938}{6}\times100 = 32.3$.

Pruebas previas

Antes de extraer los factores, debo hacer pruebas para entender la distribución de los datos y saber si es posible extraer factores. Estas prueba son:

• Prueba de esfericidad de Bartlett
• Medida de adecuación muesral de Kaiser-Meyer-Olkin (KMO)

Esfericidad de Bartlett

Esta prueba contrasta si la matriz $R$ es una matriz identidad.

Una matriz de identidad de dimensión $p \times p$ es aquella en la que todos los elementos de la diagonal son 1 y todos los elementos fuera de la diagonal son 0. Por ejemplo, para $p=3$:

$$I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

En el contexto de la prueba de esfericidad de Bartlett, contrastar si la matriz de correlaciones $R$ es la matriz identidad equivale a preguntarse si todas las variables están no-correlacionadas. Es decir, si las correlaciones fuera de la diagonal son 0.

La hipótesis nula de la prueba de Bartlett es que $R = I$. Si la prueba nos indica que $R$ difiere significativamente de la identidad, eso significa que sí hay correlaciones relevantes entre las variables, y por tanto es razonable continuar con el análisis factorial.

Prueba de KMO

Esta prueba compara las correlaciones de orden cero, es decir, las que no tienen correlación, con las correlaciones más altas entre las variables dependientes.

El valor de esta prueba tiene un rango entre 0 y 1, donde un valor menor de 0.50 se considera no-adecuado, y un valor de 0.80 o mayor se considera adecuado.

Es decir, si una correlación ofrece un valor menor de 0.50, no merece la pena someterlo a análisis factorial.

Extracción de factores

Una vez que se confirma que los datos son adecuados, se procede a la extracción de factores. Esto implica encontrar la mejor forma de representar la matriz de correlaciones $\mathbf{R}$ a partir de un conjunto reducido de factores latentes.

En análisis factorial, el objetivo es descomponer la matriz de correlaciones $\mathbf{R}$ (o su versión reducida $\mathbf{R}^*$) como:

$$R \approx \Lambda \Lambda' + U, \quad \text{o} \quad R^* \approx \Lambda \Lambda'$$

Donde:

• $\Lambda$ es la matriz de cargas factoriales.
• $\Lambda'$ es su transpuesta.
• $U$ es la matriz de unicidades.

Encontrar la matriz que reproduce $\mathbf{R}$ significa estimar los parámetros (cargas factoriales) de manera que $\Lambda \Lambda'$ se aproxime lo más posible a la estructura de correlaciones de los datos.

En otras palabras, "extraer factores” implica hallar los pesos factoriales que explican la correlación entre las variables observadas. Esta extracción se puede realizar mediante diferentes métodos, como:

• Máxima verosimilitud (MV) es el método más utilizado, porque es el que mejor reproduce los valores poblacionales. Además, ofrece una prueba de bondad de ajuste del modelo. Sin embargo, uno de los requisitos para utilizarlo es que las variables deben tener una distribución multivariada normal. Es decir, no es adecuado cuando no se cumple el principio de normalidad o la muestra es muy pequeña (menos de 300 sujetos).
• Mínimos cuadrados generalizados (MCG)
• Ejes principales (PAF, por sus siglás en inglés: Principal Axis Factoring).
• Análisis de Imagen
• Análisis alpha
• Mínimos cuadrados no ponderados
• Componentes principales (PCA, por sus siglás en inglés: Principal Component Analysis) es un método poco recomendado.

MV y MCG son los métodos más utilizados, porque no sólo son muy robustos, sino que además proporcionan pruebas de bondad de ajuste. El método de ejes principales tamién es una técnica robusta, pero no proporciona bondad de ajuste.

Cantidad de factores a extraer

En el AFE no se pre-establece cuantos factores hay que extraer. El análisis factorial exploratorio busca explorar todos los datos sin una teoría previa, por lo que no tiene sentido pre-determinar la cantidad. En teoría, se pueden analizar tantos factores como variables hay. Sin embargo, en la práctica se utilizan criterios estadísticos para decidir un número óptimo.

Algunas técnicas comunes para determinar este número son:

• Técnicas que utilizan los autovalores:
  • Regla de Kaiser: retener solo factores con autovalor mayor a 1. Es la regla más usada. Su limitación es que tiende a sobrestimar el nº de factores.
  • Gráfico de sedimentación (Scree Plot): se eligen los factores antes del "punto de codo" (elbow point). Es decir, los factores del gráfico hasta donde la curva cambia abruptamente de una pendiente pronunciada a una más plana. Es un procedimiento más preciso que la regla de Kaiser
  • Varianza explicada: se extraen factores hasta que se alcanza un porcentaje de varianza aceptable, por ejemplo el 70 o el 80%.
  • Análisis paralelo: es un método más avanzado donde el número de factores se obtiene generando matrices aleatorias similares a la muestra. Es decir, se generan muchas muestras aleatorias de datos y se calcula el promedio de cada autovalor en las muestras aleatorias. Esto genera un autovalor aleatorio que permite elegir el autovalor empírico en el cual hacer el corte.
• Técnicas que utilizan la bondad de ajuste: consiste en comparar la matriz extraída (parte explicada) con la matriz residual (parte no explicada). Si la parte no explicada (Re) es pequeña hay buen ajuste.
  • $\chi^2/g.l.$: en este estadístico, un valor $>3$ significa que hay un buen ajuste.
  • RMSEA (Root Mean Square Error of Approximation): en este estadístico, un valor $>0.05$ significa que hay un buen ajuste. $$RMSEA = \Large \sqrt{\frac{\frac{x^2 - \text{g.l.}}{n}}{\small \text{g.l.}}}$$

Las técnicas que utilizan bondad de ajuste son más propias del análisis factorial confirmatorio (AFC).

3. Rotar factores

La rotación de factores es una técnica utilizada en Análisis Factorial Exploratorio (AFE) para simplificar la interpretación de los factores sin cambiar la estructura subyacente de los datos.

El objetivo es hacer que las cargas factoriales ($a_{ik}$) sean más claras. Es decir: que cada variable esté fuertemente asociada a un solo factor y tenga cargas bajas en los demás.

En esencia, "rotar factores" significa cambiar la orientación de los factores en el espacio de las cargas factoriales, pero sin alterar la estructura de los datos ni la varianza total explicada.

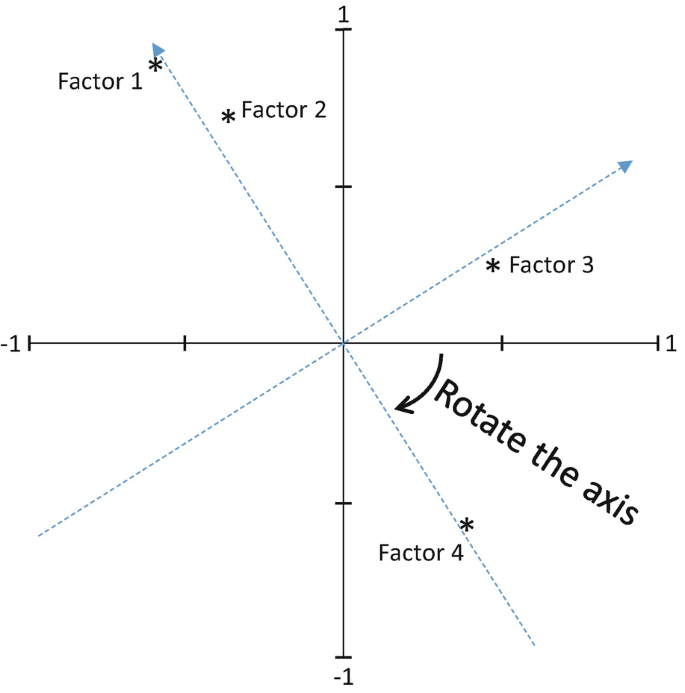
Rotar los factores no modifica la comunalidad, pero hace que los factores sean más interpretables. Es decir: no cambia el porcentaje de varianza explicado por todos los factores; pero sí cambia el porcentaje de la varianza que explica cada factor individual.

Por ejemplo, imagina la siguiente matriz de correlaciones. Puedo decir que es confusa o ruidosa, porque las cargas factoriales son similares en varios factores:

$$\Lambda = \begin{bmatrix} 0.50 & 0.45 \\ 0.48 & 0.42 \\ 0.51 & 0.47 \\ 0.45 & 0.50 \end{bmatrix}$$

Puedo rotar los datos con una rotación Varimax, hasta que encuentro una matriz en la que es más claro que las primeras dos variables están asociadas al Factor 1, y las últimas dos al Factor 2. El ruido ha disminuido porque las cargas factoriales no están dispersas entre varios factores:

$$\Lambda' = \begin{bmatrix} 0.80 & 0.10 \\ 0.75 & 0.15 \\ 0.10 & 0.82 \\ 0.12 & 0.79 \end{bmatrix}$$

Antes de la rotación, la estructura factorial puede ser difícil de interpretar, con factores que parecen mezclar distintas variables. Después de la rotación, los factores se "limpian", asignando cada variable más claramente a un solo factor.

Esto ayuda a identificar constructos latentes reales, en lugar de factores artificiales creados por correlaciones entre múltiples variables.

Tipos de rotación

Existen diversos métodos de rotación (ortogonales como Varimax, o oblicuos como Oblimin, Promax…). La elección de uno u otro depende tanto de consideraciones estadísticas (ajuste, tamaño muestral) como teóricas (si esperamos factores correlacionados o no).

• Transformaciones ortogonales: son rotaciones perpendiculares, de 90º. Son apropiadas si se espera que los factores sean independientes entre sí; por ejemplo, en pruebas de inteligencia donde los factores pueden representar habilidades separadas como verbal y numérica. Hay tres tipos de rotaciones octogonales: en función de qué buscan optimizar:
  • Varimax: Es la más usada. Maximiza la varianza de las cargas factoriales dentro de cada factor.
  • Quartimax: Minimiza el número de factores necesarios para explicar cada variable.-
  • Equamax: combinación entre Varimax y Quartimax.
• Transformaciones oblicuas: son rotaciones distintas de 90º. Son apropiadas se espera que los factores estén correlacionados; por ejemplo en rasgos de personalidad del Big Five, donde "amabilidad" y "responsabilidad" pueden compartir algo de varianza.
  • Oblimin: muy utilizada cuando se asume que los factores están relacionados. Permite encontrar estructuras factoriales más realistas en psicología y ciencias sociales.
  • Promax: similar a Oblimin, pero computacionalmente más rápida.

4. Interpretar los factores

Ahora que tengo los pesos factoriales, debo averiguar si son estadísticamente significativos. Los pesos factoriales son, en esencia, el grado en el que el factor latente explica las puntuaciones observadas. Por lo tanto, quiero saber si este grado es estadísticamente significativo.

Para que sean estadísticamente significativas, lo que significa que su valor no se debe a la aleatoriedad, puedo utilizar un criterio de significancia. Este criterio es comprobar si el peso factorial cae dentro de la zona crítica.

La zona crítica para que una correlación $\rho_{xy}$ sea significativa está definida por la siguiente fórmula:

$$|\rho_{xy}| \geq Z_{\alpha/2} \frac{1}{\sqrt{N - 1}}$$

Donde:

• $\rho_{xy}$ es la correlación entre la variable y el factor.
• $Z_{\alpha/2}$ es el valor crítico de la distribución normal estándar, correspondiente al nivel de significancia deseado (por ejemplo, para $\alpha = 0.05$, $Z_{0.025} = 1.96$).
• $N$ es el tamaño de la muestra.

Recomendaciones

Stevens (2002) aconseja interpretar sólo los pesos factoriales superiores a 0.40 y con comunalidad entre la variable oservada y el factor >15%.

Ferrando y Anguiano (2010) recomiendan:

• No utilizar muestras inferiores a 200 sujetos para que el error no sea muy alto.
• Utilizar al menos 4 variables para cada factor.
• Contrastar modelos teóricos de pocos factores.
• Utilizar variables marcadoras: variables que pesan en un solo factor y contrastadas empíricamente.
• Evitar incluir variables redundantes.
• Emplear variables con validez de contenido del factor

Por otro lado, es importante realizar una validación cruzada. Hay dos maneras de hacer esto:

• analizar otras muestras distintas de aquellas analizadas para ver si la estructura factorial se repite
• dividir la muestra usada en varias sub-muestras para ver si la estructura factorial se repite

5. Pronosticar las puntuaciones factoriales

Ahora que tengo las cargas factoriales significativas y los factores relevantes, puedo predecir la puntuación de nuevos sujetos en cada factor. Es decir, el nivel de un sujeto en el constructo.

La puntuación factorial en cada factor se calcula como una combinación lineal de las puntuaciones individuales ($X_p$) ponderadas por sus pesos factoriales ($a_{pi}$):

$$F_k = \sum_{i=1}^{p} X_i \cdot a_{ik}$$

Donde:

• $F_k$ es la puntuación factorial en el factor $k$.
• $X_i$ es la puntuación de la persona en la variable $i$.
• $a_{ik}$ es la carga factorial de la variable $i$ en el factor $k$.
• $p$ es el número de variables.

Aplicando esta fórmula a cada uno de los factores, utilizando las puntuaciones de un sujeto, puedo pronosticar su puntuación en el factor latente.

Ecuación fundamental del análisis factorial

En análisis factorial clásico, se suelen estandarizar las variables. Esto significa que se ha restado la media de esa variable a todos los valores. Dicho de otra manera, que la varianza es igual a $1$. Siendo así, una variable observable $X_p$ se puede expresar como combinación lineal de $k$ factores comunes y un término de error (o unicidad):

$$X_p = a_{p1} \cdot F_1 + a_{p2} \cdot F_2 + \dots + \boxed{a_{pk} \cdot F_k + u_p \cdot E_p}$$

donde:

• $a_{pi}$, como $a_{p1}$, $a_{p2}$... son las cargas factoriales (o factor loadings).
• $F_i$, como $F_1$, $F_2$... son los factores comunes.
• $E_p$ es el término de error (o factor específico) de la variable $p$.
• $u_p$ es el peso del error (también se asocia a la unicidad).

Notación p y k

En esta ecuación, se utiliza $p$ para denotar variables observadas. Es habitual utilizar $p$ para referirse al índice de las variables observadas.

$$X_1, X_2, X_3 ... \implies X_p$$

Por otro lado, se utiliza $k$ para los factores:

$$F_A, F_B, F_C ... \implies F_k$$

Esta notación es así por convención. No hay un motivo implícito, sino que es una decisión arbitraria muy común en la literatura.

La ecuación fundamental se expresa como una ecuación en la que las variables observables están ponderadas por unos pesos y a la que se suma la unicidad:

$$X_p = a_{pk} \cdot F_k + u_p \cdot E_p$$

• $X_p$ representa la variable observable número $p$. Suele ser un ítem o prueba estandarizada (con varianza igual a 1).
• $a_{pk}$ es la carga factorial (o peso factorial) de la variable $p$ en el factor número $k$. Cuantifica cuánto influye el factor $F_k$ en la variable $X_p$.
• $F_k$ es el factor latente número $k$. Se considera no observable directamente; se infiere a partir de las correlaciones entre las variables.
• $u_p$ es el coeficiente de la parte no explicada por los factores (es decir, la raíz de la unicidad de $X_p$). Indica la magnitud del “error” o factor específico asociado a la variable $p$.
• $E_p$: es el término de error (o factor específico) de la variable $p$. Suele asumirse como una variable aleatoria estandarizada (media 0, varianza 1), independiente de los factores comunes.

Si estimamos estas puntuaciones para cada sujeto, hablamos de puntuaciones factoriales (factor scores), que no deben confundirse con las cargas factoriales.

Varianza de las variables observadas

Si las variables están estandarizadas ($\sigma^2(X_p)=1$), entonces:

$$1 = \sigma^2(X_p) = \sum_{i=1}^k a^2_{pi} + u_p^2$$

De esta ecuación se desprenden dos conceptos importantes del análisis factorial: la comunalidad ($h^2_p$) y la unicidad ($1-h^2_p$):

• Comunalidad ($h_p^2$): parte de la varianza de $X_p$ explicada por los factores comunes. Es decir, $\sum_{i=1}^k a_{pi}^2$ es la comunalidad de la variable $p$, y se representa por $h_p^2$.
• Unicidad ($1 - h_p^2$): parte que no se explica por los factores comunes (incluye error de medida y/o variabilidad específica). Es decir, $u_p^2$ es la unicidad de la misma variable.

$$1 = \sigma^2(X_p) = \boxed{\sum_{i=1}^k a^2_{pi} = h^2_p} + \boxed{u^2_p = 1-h^2_p}$$

Se asume que $u_p^2 \ge 0$. Si llega a superar 1, se produce un caso Heywood, que indica un problema serio de ajuste o una mala especificación del modelo.

Matrices de correlaciones

En un análisis factorial, solemos trabajar con la matriz de correlaciones de las variables observables (denotada $R$), que es de dimensión $p \times p$ si tenemos $p$ variables. El objetivo es descomponer $R$ en la parte explicada por los factores comunes y la parte atribuible a unicidades (error).

Matriz de correlaciones original (R)

$R$ es la matriz de correlaciones entre las variables $X_p$. Esta matriz tiene en cuenta la varianza de los factores comunes ($A$) y la unicidad ($U$).

$$R = \Lambda \Lambda^{\prime} + U$$

donde:

• $\Lambda$ es la matriz de cargas factoriales (dimensión $p \times k$)
• $\Lambda^{\prime}$ es la matriz de cargas factoriales (dimensión $p \times k$)
• $U$ la matriz diagonal de unicidades (dimensión $p \times p$).

Es decir:

La matriz se representa de la siguiente manera:

$$R = \begin{pmatrix} 1 & 0.60 & 0.05 \\ 0.60 & 1 & 0.02 \\ 0.05 & 0.02 & 1 \end{pmatrix}$$

Como se puede ver, la diagonal contiene los valores de correlación de cada variable consigo misma ($r = 1$). Los valores fuera de la diagonal muestran la correlación entre pares de variables. Por ejemplo, la correlación entre la Variable 1 y la Variable 2 es $0.60$.

Matriz de correlaciones reducida (R^*)

La matriz de correlaciones reducida representa la parte de la correlación explicada sólo por los factores comunes, sin la unicidad. El análisis factorial busca estimar $\Lambda$ y $U$ que reproduzcan lo mejor posible $R$.

Denotada habitualmente como $R^*$, también se denomina matriz reproducida por factores. Matemáticamente, se puede expresar de la siguiente forma:

$$R^* = \Lambda \Lambda^{\prime}$$

donde

• $\Lambda$ es la matriz de cargas factoriales (dimensión $p \times k$)
• $\Lambda'$ su traspuesta ($k \times p$).

En contraste, la matriz de correlaciones original $R$ se descompone en la parte de los factores comunes más la parte de errores o varianza no compartida: $R = \Lambda, \Lambda' + U$, donde $U$ es una matriz diagonal de orden $p \times p$ que recoge las unicidades (o errores específicos) de cada variable.

A modo de ejemplo, supongamos que tenemos tres variables ($p = 3$) y un solo factor ($k = 1$) con las siguientes cargas:

• $a_{1} = 0.8$
• $a_{2} = 0.7$
• $a_{3} = 0.1$

Entonces,

$$\Lambda = \begin{pmatrix} 0.8 \\ 0.7 \\ 0.1 \end{pmatrix} \quad \Rightarrow \quad R^* = \Lambda \,\Lambda^\prime = \begin{pmatrix} 0.8 \\ 0.7 \\ 0.1 \end{pmatrix} \times \begin{pmatrix} 0.8 & 0.7 & 0.1 \end{pmatrix}$$

La multiplicación resulta en:

$$R^* = \begin{pmatrix} 0.64 & 0.56 & 0.08 \\ 0.56 & 0.49 & 0.07 \\ 0.08 & 0.07 & 0.01 \end{pmatrix}$$

Fíjate en la diagonal: aquí los valores no son 1, sino las varianzas explicadas por el factor (por ejemplo, $0.8 \times 0.8 = 0.64$). Los elementos fuera de la diagonal reflejan la correlación explicada entre cada par de variables por el factor común (p. ej., $0.8 \times 0.7 = 0.56$ para la correlación entre variables 1 y 2).

AF de orden superior

Un factor es una variable latente que explica la varianza de las variables observadas. Sin embargo, puede haber factores latentes que expliquen la varianza de los factores latentes. Es decir: hay un orden de factores.

El Análisis Factorial de Segundo Orden es una técnica utilizada para reducir una estructura factorial de primer orden, es decir, agrupar factores de primer orden en un solo factor de orden superior.

En un análisis factorial estándar (primer orden), los factores latentes explican la variabilidad de un conjunto de variables observadas (VD).

En un factorial de segundo orden, se investiga si estos factores de primer orden están relacionados entre sí, y si pueden ser explicados por un factor de orden superior.

Imagina un test de inteligencia con múltiples pruebas en diferentes habilidades:

• Factores de primer orden:
  • $F_1$ = Inteligencia espacial
  • $F_2$ = Inteligencia verbal
  • $F_3$ = Inteligencia numérica

Si estos factores están correlacionados, podemos definir un factor de segundo orden llamado "Inteligencia General" (g), que agrupa los factores más específicos.